


A key theorem of Universal Grammar is that lines do not cross in tree diagrams. However, critics of Universal Grammar challenge even such a basic result as this on the basis of sentences such as the following, taken from Virgil’s Eclogues:
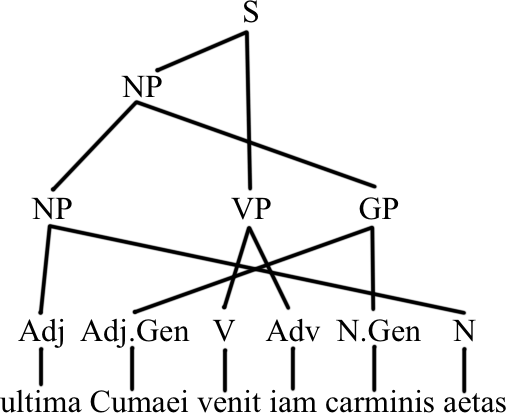
Leaving aside the fact that such forays into historical linguistics tell us nothing about the necessarily synchronic nature of Universal Grammar, we must address the fact that a naive attempt to parse this sentence leads to profoundly unsatisfactory results, as seen in Figure 1.
Sceptics claim that this shows that Latin phrases are bound together by dependency relationships rather than constituency relationships. This hypothesis, however, assumes that morphology is governing syntax, in a clear violation of the natural hierarchy of information structures. A more rigorous, mathematical approach provides a better solution.
While the surface structure of language is linear, the existence of tree diagrams shows that this structure is embedded in a 2-dimensional surface. Were it not so, we should be incapable of any grammar other than clause chaining. For convenience, this surface is usually depicted as a simple plane. However, just as the linear structure is embedded in a 2-dimensional surface, the surface may itself be embedded in 3-dimensional space. This allows us to envisage it as a curved surface, such as a torus, familiar as the shape of a doughnut, or alternatively a coffee cup.
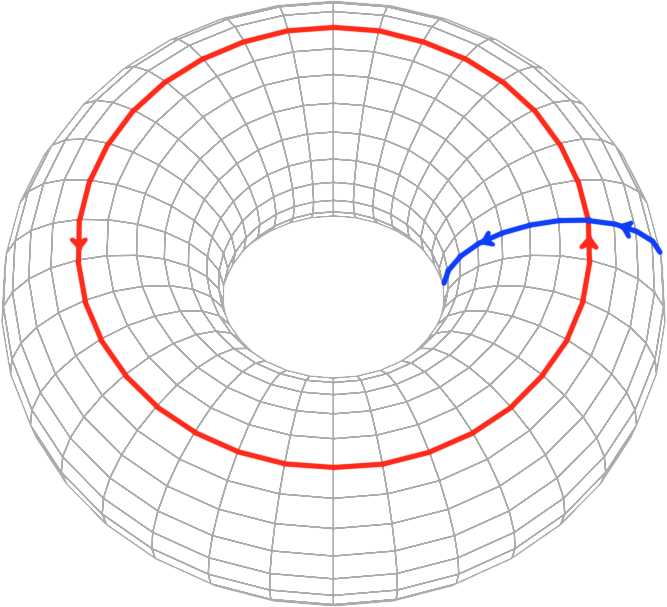
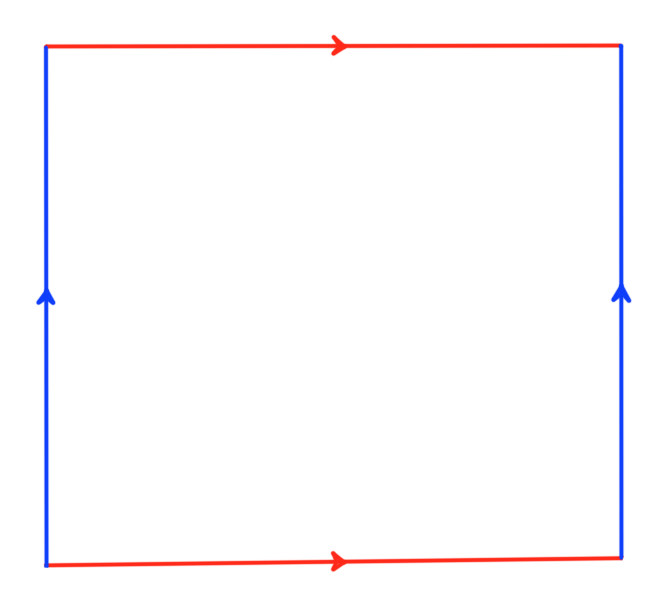
Figure 2: A torus and its representation as a topological diagram
The topological diagram in Figure 2 represents how a torus may be constructed from a flat sheet by joining opposite edges. That corresponding arrows point in the same direction indicates that the torus is an orientable surface, non-

Nothing could be simpler.